from The Worldview Literacy Book   copyright 2009            back to worldview theme #13

     Separated from their surroundings by a boundary—mass, energy, and information flow both into and out of a system. These are also transferred within the system between its component parts.  While examples of systems can be found everywhere throughout the natural, manmade, and conceptual worlds, they vary greatly in complexity. 

     In the natural world, cells, an animal's circulatory system, the human brain, eco-systems, and the Earth can be understood as systems.  In the manmade world, we can similarly consider household cooling systems, automobile braking systems, computers, automobiles, and buildings.  In the conceptual realm, computer models simulate real systems that exist in natural and manmade realms along with parts of the human societal framework.  Examples  include models of traffic flow in a city, a public social security system, and a national economy.  Many terms can be used to name, characterize and distinguish systems, including control, feedback (see Figures #13b, 13c, 31b), dynamic, linear, non-linear, chaotic, complex, hard, soft, and evolutionary.

      As the above examples suggest, many systems are themselves composed of systems (called subsystems).  Particularly complex systems may have many levels of organization.  Consider the Earth.  Studying its living things can be done at various levels: from whole biosphere perspective, to ecosystem, community, habitat, population, organism, organ, tissue, cell, down to the level of molecules inside cells.  Sometimes, in seeking to understand systems at different levels, unexpected properties emerge when higher levels of complexity are considered— properties that can't be predicted from lower level considerations.  It seems the whole system is not equal to the sum of its parts!  An example of an emergent property would be if the Earth were found to be alive and functioning as a single living organism (the Gaia hypothesis, which few take  seriously!)  Some connect emergence with God's work. 

     Rather than using old fashioned analytical, reductionist techniques for such investigation, computer models do a better job.  Indeed, constructing a program that inputs properties of a system's lower level component parts and uses understanding of how the system functions to predict behavior (provide output) at a higher level is a useful tool for discovering unexpected system behavior.  Or the process can work the other way: sometimes system behavior present at one level isn't under-stood based on the understanding of processes occurring at the lower level.  The details of how spiral arms form in galaxies were unraveled in this manner.  Perhaps the ultimate related "emergent properties" type problem is "How does human consciousness arise?"  In both investigating how the brain works and the development of artificial intelligence, neural network computer models,                              

which like the brain learn from experience, are often employed.

     Computer models and systems thinking are increasingly applied to human societal problems.  Economists use these tools to simulate and understand nearly every conceivable aspect of the free market system.  It isn't an exaggeration to say billions of dollars are often staked on the predictions that emerge from their models.  While models relevant to economic concerns have become increasingly important, so have those relevant to environmental concerns (Figure #13c).  Indeed, after inputting "business as usual" trends, output from models of the Earth's energy balance (predicted future global temperatures) is already redirecting billions of dollars of economic investment.  Human society is steadily being better understood, shaped, and in some cases redesigned by modeling the social systems involved.  Given the complexity of many of these systems, the fact that key aspects of them often are "soft" and can't even be quantified, at some point what systems thinkers do becomes less science and more art.  "Dancing With Systems" is what Donella Meadows, who inspired this theme, called it. 

     Meadows was a protégée of MIT's Jay Forrester—as was Peter Senge.  Senge pioneered in applying systems thinking to how organizations can learn and adapt—something he called "The Dance of Change."  He recognized that learning relies on a feedback loop  (see Figure #13a): a system with inputs (perceptions, reflections), outputs (actions taken), feedback and inter-relations.  Realizing that the key aspect of organizational learning is the interaction between its individuals, Senge's 1990 book The Fifth Discipline identifies five learning disciplines to promote the desired group problem solving. 

     In summarizing these disciplines he writes, "Building shared vision fosters a commitment to the long term.  Mental models focus on the openness needed to unearth shortcomings in our present ways of seeing the world.  Team learning develops the skills of groups of people to look for the larger picture that lies beyond individual perspectives.  And personal mastery fosters the personal motivation to continually learn how our actions affect our world.  Lastly, systems thinking makes understandable the subtlest aspect of the learning organization—the new way individuals perceive themselves and their world.  At the heart of a learning organization is a shift of mind—from seeing ourselves as separate from the world to connected to the world, from seeing problems as caused by someone or some-thing 'out there' to seeing how our own actions create the problems we experience."  Senge thinks in terms of circles of causality, and writes, "Reality is made up of circles, but we see straight lines.  Herein lie the beginnings of our limitation as systems thinkers."  

Figure #13a

The Learning Cycle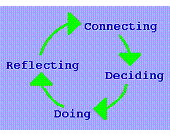

Figure #13c

Positive Feedback Loops in Global Climate Models

1) Albedo Feedback: Albedo refers to the % incident sunshine that is reflected back from a surface.  As global warming increases temperatures, highly reflective polar sea ice melts--replaced by darker ocean water.  This lowering of the albedo results in more solar energy absorbed (darker surfaces are better absorbers), higher temperatures, more ice melting, etc.

Figure #13b: Positive & Negative Feedback Loops